The series of String Math conferences
The series of String Math conferences has developed into a central event on the interface between mathematics and physics related to string theory, quantum field theory and related topics. The conferences have been organized annually since 2011; the conference in 2022 is organized at the Faculty of Physics, University of Warsaw (Pasteura Street 5, 02-093 Warsaw, Poland). The list of previous String Math conferences is here. The next String Math conference will take place on July 10-14, 2023, at the University of Melbourne in Australia.

The University of Warsaw
The University of Warsaw, founded in 1816, is the largest university in Poland and a leading research centre in the country and in this region of Europe. The Faculty of Physics and the Faculty of Mathematics, Informatics, and Mechanics, are regarded as one of the best in the country, and are recognized internationally for the high quality of research and education. The university is located in the capital of Poland, one of the most dynamically developing European cities. Warsaw is the centre of political and economic life and has a lively social and cultural scene.
Program
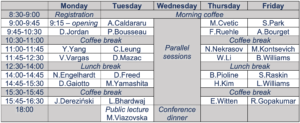
Conference schedule
Invited lectures – titles and abstracts
Lakshya Bhardwaj (University of Oxford)
Title: Non-Invertible Symmetries and Higher-Categories
Abstract: Currently, there is a strong interest in the study of non-invertible symmetries of quantum field theories. These symmetries vastly generalize the standard notion of global symmetries, and can be used in a similar way to obtain insights into strongly-coupled physical phenomena. It is expected that the right mathematical structure to capture physical properties of such symmetries is that of higher-categories. In this talk, we will discuss recent progress in constructing explicit examples of higher-categories describing non-invertible symmetries in quantum field theories of various spacetime dimensions ranging from d=3 to d=6. These higher-categories are constructed by equivariantizing higher-categories corresponding to invertible higher-form symmetries.
[Slides] [Video]
Antoine Bourget (CEA Saclay)
Title: Magnetic quivers for Superconformal Field Theories
Abstract: Superconformal field theories with 8 supercharges in spacetime dimensions 3 to 6 have a large moduli space of vacua. The hyperKahler branches can be characterized by a combinatorial object known as a magnetic quiver. It fully encodes the geometry, and a simple algorithm allows access to the structure of nested singularities, which corresponds physically to a generalized Higgs mechanism. I will illustrate this construction on examples of low rank 4d N=2 SCFTs.
[Slides] [Video]
Pierrick Bousseau (ETH Zürich)
Title: Holomorphic Floer theory and Donaldson-Thomas invariants
Abstract: Holomorphic Floer theory is the analog of Floer theory for holomorphic symplectic manifolds. This topic has been recently explored, from several different perspectives, by Kontsevich-Soibelman and Doan-Rezchikov. In a different direction, I will in this talk present a conjectural picture relating holomorphic Floer theory of complex integrable systems to Donaldson-Thomas invariants. In physical terms, we will discuss a relation between the BPS spectrum of an N=2 4-dimensional field theory and the enumerative geometry of the corresponding Seiberg-Witten integrable system.
[Slides] [Video]
Andrei Caldararu (University of Wisconsin Madison)
Title: Categorical Enumerative Invariants
Abstract: The theory of Categorical Enumerative Invariants (CEIs) is a non-commutative generalization of the theory of Gromov-Witten invariants. CEIs are associated to an arbitrary Calabi-Yau category, together with a splitting of the Hodge filtration. CEIs should be thought of as a precise realization of the general idea, due to Kontsevich, that the category of open strings (plus data of the splitting) determine closed string invariants. I will present a general overview of the theory of CEIs, and discuss how it provides a conjectural approach to understanding enumerative mirror symmetry for the quintic threefold, in arbitrary genus. I will also discuss a second application, a new definition of FJRW invariants in the presence of an arbitrary symmetry group.
[Slides] [Video]
Mirjam Cvetic (University of Pennsylvania)
Title: Geometry of Higher-Form Group Structures in String Theory
Abstract: By studying M-theory on singular non-compact special holonomy spaces X we demonstrate, via a process of cutting and gluing of singularities that extend to the boundary of X, the appearance of 0-form, 1-form and 2-group symmetries in the resulting supersymmetric quantum field theory. We highlight prototype examples of elliptically fibered non-compact Calabi-Yau fewfolds and comment on the fate of these symmetries when these spaces become compact.
[Slides] [Video]
Jan Dereziński (University of Warsaw)
Title: Dirac-Coulomb Hamiltonians [online talk]
Abstract: I will discuss the theory of Dirac operators perturbed by the Coulomb potential in an arbitrary dimension. These operators are interesting for several reasons:
– They have obvious applications to atomic physics.
– If one neglects the mass term, they are formally homogeneous.
– Depending on the coupling constant and dimension, they exhibit several distinct scaling behaviors (or if you prefer the high energy jargon, various “renormalization group flows”).
– Their definition involves subtle boundary conditions.
– They are exactly solvable in terms of Whittaker functions.
My talk will be based on recent joint work with Błażej Ruba.
[Slides] [Video]
Netta Engelhardt (MIT)
Title: The Penrose Inequality as Swampland Condition?
Abstract: Cosmic censorship as a conjecture about classical General Relativity is now understood to be false in both higher dimensional asymptotically flat space and four-dimensional AdS. Certain reformulations and consequences of cosmic censorship, however, may be true in asymptotically AdS solutions that admit a consistent holographic dual. I will discuss two such consequences — the Penrose Inequality and constraints on the location of trapped surfaces — as possible diagnostics for whether a given solution admits a consistent UV completion within AdS/CFT.
[Slides] [Video]
Dan Freed (University of Texas at Austin)
Title: Finite symmetry in field theory
Abstract: Recently there has been lots of activity surrounding generalized notions of symmetry in quantum field theory, including “categorical symmetries”, “higher symmetries”, “noninvertible symmetries”, etc. Inspired by definitions of abstract (finite) groups and algebras and their linear actions, we introduce a framework for these symmetries in field theory. This is joint work with Constantin Teleman and Greg Moore.
[Slides] [Video]
Davide Gaiotto (Perimeter Institute)
Title: Perturbative calculations in twisted 4d gauge theories [online talk]
Abstract: I will review the holomorphic twist of four-dimensional N=1 gauge theories and present the Feynman diagrams which control the perturbative corrections to the twisting supercharge and to the higher operations available in the twisted theories. I will describe how to bootstrap these perturbative corrections without computing actual Feynman integrals and present some preliminary results for pure N=1 gauge theory.
[Slides] [Video]
Rajesh Gopakumar (ICTS, Bangalore)
Title: Deriving Gauge-String Duality
Abstract: Gauge-String duality (or the AdS/CFT correspondence, as a special case) has wide ranging ramifications in physics as well as mathematics. I will first sketch a broad approach to systematically understand the underpinnings of this still mysterious connection between gauge theories (in the large N limit) and perturbative closed string theory. I will then summarise recent work (with Matthias Gaberdiel and others) on the AdS_3/CFT_2 correspondence, in the tensionless limit, which gives a proof of concept of the above ideas. Correlation functions in the worldsheet theory on AdS_3 are shown to agree with those of the dual CFT_2, with both being given in terms of branched covers. In the limit of large covering, we arrive at an even more fine grained picture and see how the moduli space of string worldsheets arises from the dual CFT. This is enabled by the surprising appearance of a Penner-like matrix model whose spectral curve turns out to give a Strebel differential. Finally, I will mention how some of these features are likely to persist in a proposal for the worldsheet dual of free N=4 Super Yang-Mills theory.
[Slides] [Video]
David Jordan (University of Edinburgh)
Title: Topological Langlands duality and 1-form symmetries
Abstract: The main goal of this talk is to present a novel conjectural incarnation of Langlands duality in the purely topological setting of character varieties of 3-manifolds and their quantizations via skein theory. Our conjecture, which we have developed with Ben-Zvi, Gunningham and Safronov, asserts an equality of dimensions between the G- and G^L-skein modules of a 3-manifold at generic quantization parameter. I will then outline work in progress with Gunningham and Safronov to prove the conjecture in a number of special cases. The proof in these cases uses the notion of 1-form symmetries (= co-dimension 2 topological defects) to express PGL(N)-skein modules as certain twisted SL(N)-skein-modules, and then to further relate these to well-known formulas for the cohomology of twisted character varieties of surfaces.
[Slides] [Video]
Heeyeon Kim (Rutgers University)
Title: Path integral derivations of K-theoretic Donaldson invariants
Abstract: We discuss the partition functions of topologically twisted 5d SU(2) supersymmetric Yang-Mills theory on X x S1, where X is a smooth closed four-manifold. Mathematically, they can be identified with the K-theoretic versions of the Donaldson invariants on X. In particular, we provide two different path integral derivations of their wall-crossing formula for b_2^+(X)=1. We also discuss generalizations to b_2^+(X)>1.
[Slides] [Video]
Maxim Kontsevich (IHÉS)
Title: Spectrum in quantum mechanics and deformed periods [online talk]
Abstract: About 40 years ago J. Zinn-Justin formulated several conjectures about the perturbative expansion of the spectrum a quantum Hamiltonian (for the polynomial potential in 1 variable). In particular, he discovered a hidden structure governed by Bernoulli numbers. I’ll explain this phenomenon, and propose a new effective algorithm for the calculation of the spectrum which is not based on quantum algebra at all (joint work in progress with A. Soibelman).
[Slides] [Video]
Conan Leung (Chinese University of Hong Kong)
Title: Smoothing, scattering and a conjecture of Fukaya [online talk]
Abstract: In 2002, Fukaya proposed a remarkable explanation of mirror symmetry detailing the SYZ conjecture by introducing two correspondences: one between the theory of pseudo-holomorphic curves on a Calabi-Yau manifold Xˇ and the multi-valued Morse theory on the base Bˇ of an SYZ fibration pˇ : Xˇ → Bˇ, and the other between deformation theory of the mirror X and the same multi-valued Morse theory on Bˇ. We prove a reformulation of the main conjecture in Fukaya’s second correspondence, where multi-valued Morse theory on the base Bˇ is replaced by tropical geometry on the Legendre dual B. This is a joint work with Kwokwai Chan and Ziming Ma.
[Slides] [Video]
Wei Li (Chinese Academy of Sciences)
Title: From BPS crystals to BPS algebras
Abstract: I will explain how to construct BPS algebras for string theory on general toric Calabi-Yau threefolds, based on the crystal melting description of the BPS sectors. The resulting quiver Yangians, together with their trigonometric and elliptic versions, unify various known results and generalize them to a much larger class. I will then explain how to describe their representations using subcrystals and how they can be translated into the framings of the quivers. Finally, I will discuss some applications.
[Slides] [Video]
Dalimil Mazac (IAS)
Title: Automorphic Spectra and the Conformal Bootstrap
Abstract: I will describe a close analogy between the spectral geometry of hyperbolic manifolds and conformal field theory. A hyperbolic d-manifold gives rise to a Hilbert space which is a unitary representation of the conformal group in d-1 dimensions. Elements of this Hilbert space can be thought of as local operators living in a (d-1)-dimensional spacetime. Their scaling dimensions are related to the Laplacian eigenvalues on the manifold. The operators satisfy an operator product expansion. One can define correlation functions and derive conformal bootstrap equations constraining the spectrum. As an application, I will use conformal bootstrap techniques to obtain new rigorous bounds on the first positive Laplacian eigenvalue of hyperbolic orbifolds. In two dimensions, these bounds allow us to determine the set of first eigenvalues attained by all hyperbolic orbifolds. Based on joint work with Petr Kravchuk and Sridip Pal.
[Slides] [Video]
Nikita Nekrasov (Simons Center for Geometry and Physics)
Title: Knizhnik-Zamolodchikov revisited: (non)supersymmetric gauge theories, defects, and localization
Abstract: Knizhnik-Zamolodchikov equation, originally found in the context of a two dimensional conformal field theory, has recently been found in the context of instanton counting, albeit with a significantly extended domain of allowed parameters (level, spins etc). I will also explain how the Hecke operators from geometric and analytic Langlands correspondence are realized in the four dimensional super-Yang-Mills theory. Extending this story, I will talk about other physical realizations of “analytically continued” systems, such as Regge poles, replicas, or dimensional regularization. I will also touch upon the issue of the Lorentzian vs Euclidean metric slice in the path integral contour of quantum gravity.
[Slides] [Video]
Sunghyuk Park (California Institute of Technology)
Title: Homological blocks and R-matrices
Abstract: Homological block, commonly denoted by ẑ, is a 3-manifold invariant whose existence was predicted by S. Gukov, D. Pei, P. Putrov, and C. Vafa in 2017 using 3d/3d correspondence. To each 3-manifold equipped with a spin^c structure, ẑ is supposed to assign a q-series with integer coefficients that is categorifiable and provides an analytic continuation of the Witten-Reshetikhin-Turaev invariants. In 2019, S. Gukov and C. Manolescu initiated a program to mathematically construct ẑ via Dehn surgery, and as part of that they conjectured that the Melvin-Morton-Rozansky expansion of the colored Jones polynomials can be re-summed into a two-variable series for knot complements. In this talk, I will explain how to prove their conjecture for a big class of link complements by making use of the R-matrix for Verma modules.
[Slides] [Video]
Boris Pioline (Sorbonne Université and CNRS)
Title: BPS Dendroscopy on local Calabi-Yau threefolds
Abstract: The spectrum of BPS states in D=4 supersymmetric field theories and string vacua famously jumps across codimension-one walls in vector multiplet moduli space. The Attractor Flow Tree conjecture postulates that the BPS index $\Omega(\gamma,z)$ for given charge $\gamma$ and moduli $z$ can be reconstructed from the `attractor indices’ $\Omega_*(\gamma_i)$ counting BPS states of charge $\gamma_i$ in their respective attractor chamber, by summing over all possible decompositions $\gamma=\sum_i \gamma_i$ and over decorated rooted flow trees. Physically, flow trees provide a mesoscopic representation of BPS states as nested multi-centered bound states of elementary constituents. I will present a rigorous version of this formula in the context of quivers with potential, which governs the BPS spectrum in type IIA string theory compactified on certain conical Calabi-Yau threefolds, in the vicinity of orbifold-type points in Kahler moduli space. Moving away from such orbifold points requires generalizing the flow tree formula from the Abelian category of quiver representations to the derived category of the same. I will present recent progress in this direction in the simplest case of local $P^2$, and argue that its global BPS spectrum and flow tree structure can be deduced from a scattering diagram with simple initial data.
[Slides] [Video]
Sam Raskin (University of Texas at Austin)
Title: Quantum duality and Morita theory for chiral a
Abstract: We will discuss how dualities of quantum field theories can be understood as analogous to Morita equivalences for alg
[Slides] [Video]
Fabian Ruehle (Northeastern University)
Title: Approximations for Calabi-Yau and other special holonomy/structure metrics
Abstract: I will discuss methods to numerically approximate Ricci-flat metrics for Calabi-Yau n-folds defined as complete intersections in toric ambient spaces. The two-step procedure involves first finding points on the Calabi-Yau manifold and then approximating the Ricci-flat metric by approximating solutions to the underlying Monge-Ampere equation. Possible applications include computing massive string excitations, volumes of non-calibrated cycles, the SYZ conjecture, and approximating solutions to the Hermitian Yang-Mills equations. The methods can also be extended to SU(n) or G2 structure metrics
[Slides] [Video]
Vincent Vargas (University of Geneva)
Title: Liouville conformal field theory: from the probabilistic construction to the bootstrap construction
Abstract: Liouville field theory was introduced by Polyakov in the eighties in the context of string theory. Liouville theory appeared there under the form of a 2D Feynman path integral and since then has appeared in a wide variety of contexts (random conformal geometry, SUSY Yang-Mills, etc…). Recently, a rigorous probabilistic construction of the path integral was provided using the Gaussian Free Field. In this talk, I will review the probabilistic construction and its equivalence with the bootstrap construction used in the physics literature. The key steps in this equivalence is a probabilistic derivation of the DOZZ formula for the structure constants, the spectral analysis of the Hamiltonian of the theory and the proof that the probabilistic construction satisfies certain natural geometrical gluing rules called Segal’s axioms. Based on numerous works with G. Baverez, F. David, C. Guillarmou, A. Kupiainen, R. Rhodes.
[Slides] [Video]
Brian Williams (University of Edinburgh)
Title: A holomorphic approach to fivebranes
Abstract: The six-dimensional superconformal field theory associated to an ADE Lie algebra plays a key role in the AGT correspondence. Its explicit description as a QFT has remained elusive. Motived by (twisted) holography (following Costello, Gaiotto, Li, and Paquette) we find a holomorphic model describing the minimal twist of the six-dimensional theory. From this description, we propose a symmetry for the space of instantons on C^2 by an exceptional super Lie algebra called E(3|6). In the case of rank one instantons this factors through a `Heisenberg’ type super Lie algebra and the story is analogous to Nakajima’s action on the Hilbert scheme. This is based on joint work with Raghavendran.
[Slides] [Video]
Lauren Williams (Harvard University)
Title: The positive Grassmannian, amplituhedron, and cluster algebras [online talk]
Abstract: The positive Grassmannian Grk,n≥0 is the subset of the real Grassmannian where all Plücker coordinates are nonnegative. It has a beautiful combinatorial structure as well as connections to statistical physics, integrable systems, and scattering amplitudes. The amplituhedron An,k,m(Z) is the image of the positive Grassmannian Grk,n≥0 under a positive linear map Rn→Rk+m. We will explain how ideas from oriented matroids, tropical geometry, and cluster algebras shed light on the structure of the positive Grassmannian and the amplituhedron.
[Slides] [Video]
Edward Witten (IAS)
Title: Algebras and Entropies
Abstract: It has been found, originally in the context of black hole thermodynamics, that the concept of “entropy” is better-defined in the presence of gravity than in ordinary quantum field theory without gravity. In this talk, I will give a slightly abstract explanation of this phenomenon, at least for the case of a black hole.
[Slides] [Video]
Mayuko Yamashita (Kyoto University)
Title: Category of QFTs and differential cohomology
Abstract: Recently, higher categorical understandings of quantum field theories have been rapidly developing. On the other hand, differential cohomology theories, whose relationships with physics are classical, are most modernly understood in terms of sheaves on manifolds with values in (\infty, 1)-categories. In this talk, I explain an ongoing work to combine them, and to give a higher relations between QFTs and differential cohomology. Invertible QFTs are expected to form a sheaf of \infty-groupoids, and we apply the framework of differential cohomology to this sheaf. This is a joint work with K. Ohmori (U. Tokyo).
[Slides] [Video]
Yaping Yang (University of Melbourne)
Title: Cohomological-type Hall algebras and their representation theory
Abstract: I will review the Cohomological Hall algebra associated to a quiver and an oriented cohomology theory. This construction gives rise to new quantum groups. In my talk, I will discuss the following two examples. When the cohomology theory is the Morava E-theory, we obtain a new family of quantum groups labelled by a prime number and a positive integer. I will discuss a phenomenon similar to Frobenius of modular representation theory. When the quiver comes from a smooth local toric Calabi-Yau 3-fold, we obtain a generalization of shifted Yangian, which acts on the cohomology of the moduli space of certain sheaves of the 3-fold. This gives the symmetry algebra action on the categorified DT.
[Video]
Parallel sessions
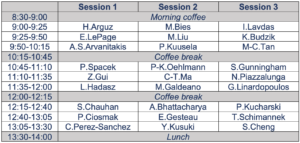
Schedule of parallel sessions (Wednesday, July 13)
Session 1
Hulya Arguz (IST Austria)
Title: The higher dimensional tropical vertex
Abstract: Gross and Siebert developed a program for understanding mirror symmetry algebro-geometrically. In this talk, we will explain how to compute concrete equations of mirrors to blow-ups of toric varieties in the framework of the Gross–Siebert program. This uses a combinatorial algorithm computing certain types of Gromov–Witten invariants encoded in a scattering diagram. This is joint work with Mark Gross.
[Slides]
Elise LePage (University of California, Berkeley)
Title: Calculating Quantum Knot Homology from Homological Mirror Symmetry
Abstract: I will explain how to explicitly calculate knot homology using the Fukaya category associated to a 2d Landau-Ginsburg theory, which is the equivariant mirror of the Coulomb branch of a 3d $mathcal{N}=4$ theory. For different choices of superpotential, the LG theory categorifies the quantum knot invariants associated with any simply-laced Lie algebra. The knot homology is calculated from homs between particular branes, and we are able to construct projective resolutions of these branes in terms of thimbles, making the computation entirely algebraic. We also provide the action of braiding on the relevant branes, so we can calculate Khovanov homology for any knot given its braid representation. I will show how this calculation works for su(2) and give an example. This approach is based on 2105.06039 and is joint work with Aganagic and Rapcak.
[Slides]
Alex S. Arvanitakis (Vrije Universiteit Brussel)
Title: On topology change in Poisson-Lie T-duality
Abstract: I will be discussing my recent work [2110.08179] with Chris Blair and Dan Thompson on topology change in Poisson-Lie T-duality with spectators (i.e. where the dualisable dimensions are fibred over a `spectator’ base). We can exhibit for instance a duality between a trivial bundle with abelian isometries and a non-trivial *bibundle* with a nonabelian Poisson-Lie group action. This will be done in the language of QP manifolds/symplectic L-infinity algebroids which is convenient for showing the duality is a canonical transformation in string phase space, and also provides glimpses of a generalisation towards U-duality and higher branes.
[Slides]
Peter Spacek (TU Chemnitz)
Title: Landau-Ginzburg models for cominuscule homogeneous spaces
Abstract: We will present type-independent Laurent polynomial LG-models for the (small) quantum cohomology of cominuscule spaces [Spacek21] as well as Plücker coordinate LG-models for the exceptional family [Spacek-Wang22]. These models share the general structure of the so-called “canonical LG-models”; constructed by Marsh, Pech, Rietsch and Williams for Grassmannians, Lagrangian Grassmannians and quadrics, and we will discuss our ongoing efforts in unifying the models into a type-independent canonical model. Time permitting, we will discuss a number of related results, such as the cluster structures and Newton-Okounkov bodies determined for the exceptional family in [Spacek-Wang22], and connection to other mirror symmetry statements such as the quantum D-module isomorphism proven for minuscule homogeneous spaces in [Lam-Templier17].
[Slides]
Zhengping Gui (International Centre for Theoretical Physics)
Title: Elliptic trace map on chiral algebras
Abstract: Trace map on deformation quantized algebra leads to the algebraic index theorem. We investigate a two-dimensional chiral analogue of the algebraic index theorem via the theory of chiral algebras developed by Beilinson and Drinfeld. We construct a trace map on the elliptic chiral homology of the free beta gamma-bc system using the BV quantization framework. As an example, we compute the trace evaluated on the unit constant chiral chain and obtain the formal Witten genus in the Lie algebra cohomology. This talk is based on joint work with Si Li.
Leszek Hadasz (Jagiellonian University)
Title: Non-rational $widehat{su}(2)$ cosets and Liouville field theory
Abstract: During my presentation, I will discuss certain equivalences between conformal field theories with a continuous spectrum: Liouville theory, its supersymmetric extension, and models based on the affine su(2) algebra with irrational level.
[Slides]
Sachin Chauhan (Indian Institute of Technology, Bombay)
Title: q-series for so(3) and osp(1|2)
Abstract: Three-manifold invariants $\hat Z$ (“Z-hat”), also known as homological blocks, are $q$-series with integer coefficients. Explicit $q$-series form for $\hat Z$ is known for $SU(2)$ group, supergroup $SU(2|1)$ and ortho-symplectic supergroup $OSP(2|2)$. We focus on $\hat Z$ for $SO(3)$ group and orthosymplectic supergroup $OSP(1|2)$. Particularly, the change of variable relating $SU(2)$ link invariants to the $SO(3)$ \& $OSP(1|2)$ link invariants plays a crucial role in explicitly writing the $q$-series.
[Slides]
Paweł Ciosmak (IDEAS NCBiR)
Title: Quantum curves and vertex algebras
Abstract: Quantum curves can be associated with the singular vectors in the Verma modules over the Virasoro algebra. This relation originally developed from the point of view of matrix models, was later studied from the point of view of conformal field theory. We are going to perform a construction of such quantum curves using the mathematical language of vertex operator algebras. This construction has several advantages and opens perspectives towards generalization to the case of the $cW$-algebras
[Slides]
Carlos Perez-Sanchez (University of Heidelberg)
Title: A Yang-Mills matrix theory
Abstract: The problem of quantization of noncommutative spaces (spectral triples) is addressed first in a finite-dimensional, Euclidean setting (thus referred to as random noncommutative geometry, or Dirac ensambles). To address the problem of quantization of a space with gauge fields, first the structure that in the smooth (i.e. commutative) spacetime case is well-known to yield the Yang-Mills(-Higgs) theory, namely almost-commutative manifolds, has to be replaced by its ‘fuzzy’ counterpart already the classical level. We provide new the structure that allows this, whose quantisation turns out to be lead to a multimatrix ensemble.
[Slides]
Session 2
Martin Bies (University of Pennsylvania)
Title: Towards F-theory MSSMs
Abstract: This talk summarizes recent developments aimed towards F-theory constructions of MSSMs, i.e. F-theory vacua with exactly one Higgs field and no vector-like exotics.
[Slides]
Muyang Liu (Uppsala University)
Title: Revisiting Heterotic ALE Instantons: F-theory, 2-groups, and T-duality
Abstract: In this talk, I will revisit the construction of heterotic ALE instantons and the corresponding T-dual systems in 6D little string theories (LSTs). Considering two heterotic E8 × E8 and Spin(32)/Z2 string theory placed on various background singularities, we expect the heterotic NS5 instantons to fraction. The choice of flat connection at infinity for E8 or Spin(32)/Z2 respectively captures the feature of the 6D conformal matter theory built on F-theory geometry. We propose that the matching of 5d coulomb branches plus the 2-group structure constants determined by the higher form symmetry of LSTs as criteria to predict heterotic T-dual candidates.The exploitation are generalized by picking non-trivial flat connections at the infinity to break E8 and Spin(32)/Z2 into their subgroups and confirm these T-dualities by the matching of criteria aforementioned. In addition, distinct tensor branch data obtained from 6D theories with a single instanton inspire us to classify heterotic strings probing ADE singularities.
[Slides]
Pyry Kuusela (University of Oxford)
Title: Families of Modular Flux Vacua on Symmetric CY Threefolds
Abstract: One aspect of the relation between physics and arithmetic geometry is the conjectured correspondence between supersymmetric flux vacua and weight-2 modular CY threefolds. We present a novel construction of such flux vacua in permutation-symmetric multiparameter compactifications, and develop methods for efficiently computing the zeta functions of the corresponding geometries. In our examples we find agreement with the flux modularity conjecture of Kachru, Nally, and Yang. The CY manifolds admitting supersymmetric flux vacua can be associated to elliptic, Hilbert, or Bianchi modular forms, depending on the field the complex structure moduli of the CY take values in.
Paul-Konstantin Oehlmann (Uppsala University)
Title: Heterotic little strings, T-duality and 2-group symmetries
Abstract: We explore little string theories in six dimensions, constructed via F-theory that are dual to heterotic strings with NS5 branes probing ADE type singularities. The resulting quivers highlight fractionalization of those branes, that we determine for single and multiple brane stacks. Little string theories also possess T-duality as well as higher form- and group symmetries. We determine the T-dual theories and match those global symmetries across the dualities. We engineer these models using toric geometry techniques to construct non-compact threefolds that manifestly have multiple fibrations and hence M/F-theory lifts. T-duality then becomes a fibre-base duality of the threefold which allows us to compute the little-string-charges directly from the Kac labels of the dual gauge groups.
Chen-Te Ma (Asia Pacific Center for Theoretical Physics)
Title: Emergence of Time from Unitary Equivalence
Abstract: We implement the unitary equivalence of modular Hamiltonian $hat{H}_{mathrm{mod}}$ and Hamiltonian $hat{H}$,$hat{H}simhat{U}^{dagger}hat{H}_{mathrm{mod}}hat{U}$, to realize the emergence of time from an unitary operator $hat{U}$. The unitary equivalence relation implies a duality between the modular flow and time evolution. Requiring the unitary equivalence also implies “Modular Chaos Bound = Chaos Bound''. We demonstrate the duality of quantum chaos quantities in the thermofield double state defined in a fermionic system. We then show the explicit duality between a specific form of correlators, the spectral form factor, and the Loschmidt echo with $hat{H}_{mathrm{mod}}$. In the end, we also consider a two-qubit system to demonstrate that a different entanglement spectrum does not provide the same constraint to $hat{H}$.
[Slides]
Mateo Galdeano (University of Oxford)
Title: Families of solutions of the heterotic G2 system
Abstract: The heterotic G2 system is the 7-dimensional analogue of the Hull-Strominger system. Solutions to this system describe compactifications of heterotic string theory with N=1 supersymmetry on a 7-dimensional manifold. From a mathematical perspective, these solutions involve interesting constructions in geometry such as integrable G2-structures and G2-instantons. Unfortunately, finding explicit solutions to the system is a challenging problem due to the existence of an anomaly cancellation condition for the gauge fields. In this talk I will introduce the heterotic G2 system and show how to construct families of solutions using homogeneous 3-Sasakian manifolds with squashed metrics. This talk is based on joint work with Xenia de la Ossa, arXiv:2111.13221.
[Slides]
Aranya Bhattacharya (IISc, Bangalore)
Title: Integrability check for open quantum systems in Krylov Space
Abstract: Open quantum systems are of experimental interest since ideally real life experiments always have some interaction with its environment. Due to its interaction, the system density matrix and operators within the system Hilbert space evolve non-unitarily. We study an open quantum many body spin system to check whether its integrable and chaotic regimes can be distinguished by looking at the non-unitary dynamics of a simple operator in Krylov space.
[Slides]
Elliott Gesteau (California Institute of Technology)
Title: Holographic tensor networks from hyperbolic buildings
Abstract: Holographic tensor networks are discrete models of AdS/CFT that satisfy complementary recovery of quantum information and the Ryu-Takayanagi formula, which relates the boundary entanglement entropy to the area of extremal surfaces in the bulk. In this talk, I will construct a large class of discrete geometric structures in all dimensions that satisfy these two properties, using the theory of hyperbolic buildings. Interestingly, most of the structures uncovered have a fractal boundary at infinity, which possesses a rich geometric structure. The Ryu-Takayanagi formula then encodes the fractal dimension of the boundary, while the extremal surfaces encode an important part of the geometry of the buildings, showing a new interplay between ideas from holography and geometric group theory. This is based on arXiv:2202.01788, with Matilde Marcolli and Sarthak Parikh.
Yuya Kusuki (California Institute of Technology)
Title: Bootstrapping AdS/BCFT
Abstract: The interpretation of semiclassical gravity as an average of CFTs has provided much progress in understanding the factorization problem and the information paradox. We introduce a new idea, boundary averaging, to address the question: Does averaging also work well in AdS/BCFT? We provide significant evidence that averaging plays an important role in reproducing semiclassical gravity in AdS/BCFT. To address this issue, we use the fusion-matrix bootstrap, which is recently developed in the context of the light-cone bootstrap.
[Slides]
Session 3
Ioannis Lavdas (LMU Munich)
Title: Holomorphic boundary conditions for topological field theories via branes in twisted supergravity
Abstract: Three-dimensional N =4 supersymmetric field theories admit a natural class of chiral half-BPS boundary conditions that preserve N = (0, 4) supersymmetry. While such boundary conditions are not compatible with topological twists, deformations that define boundary conditions for the topological theories were recently introduced by Costello and Gaiotto. Not all N = (0, 4) boundary conditions admit such deformations. We revisit this construction, working directly in the setting of the holomorphically twisted theory and viewing the topological twists as further deformations. Properties of the construction are explained both purely in the context of holomorphic field theory and also by engineering the holomorphic theory on the worldvolume of a D-brane. Our brane engineering approach combines the intersecting brane configurations of Hanany–Witten with recent work of Costello and Li on twisted supergravity. The latter approach allows to realize holomorphically and topologically twisted field theories directly as worldvolume theories in deformed supergravity backgrounds, and we make extensive use of this.
[Slides]
Kasia Budzik (Perimeter Institute)
Title: Giant Gravitons in Twisted Holography
Abstract: Twisted holography relates the 2d chiral algebra subsector of N = 4 SYM to the B-model topological string theory on the deformed conifold SL(2,C). Determinant operators in the chiral algebra insert Giant Graviton branes in the dual geometry. In this talk, I will present a match between the large-N saddles of the correlation functions of determinants with semiclassical D-brane configurations in the dual theory, using a spectral curve construction. The match can be extended to saddles which appear in non-trivial Coulomb branch vacua. The talk is based on work in collaboration with Davide Gaiotto.
[Slides]
Meng-Chwan Tan (National University of Singapore)
Title: Vafa-Witten Theory: Invariants, Floer Homologies, Higgs Bundles, a Geometric Langlands Correspondence, and Categorification [online talk]
Abstract: We revisit Vafa-Witten theory in the more general setting whereby the underlying moduli space is not that of instantons, but of the full Vafa-Witten equations. We physically derive (i) a novel Vafa-Witten four-manifold invariant associated with this moduli space, (ii) their relation to Gromov-Witten invariants, (iii) a novel Vafa-Witten Floer homology assigned to three-manifold boundaries, (iv) a novel Vafa-Witten Atiyah-Floer correspondence, (v) a proof and generalization of a conjecture by Abouzaid-Manolescu about the hypercohomology of a perverse sheaf of vanishing cycles, (vi) a Langlands duality of these invariants, Floer homologies and hypercohomology, and (vii) a quantum geometric Langlands correspondence with purely imaginary parameter that specializes to the classical correspondence in the zero-coupling limit, where Higgs bundles feature in (ii), (iv), (vi) and (vii). We also explain how these invariants and homologies will be categorified in the process, and discuss their higher categorification. We therefore relate differential and enumerative geometry, topology and geometric representation theory in mathematics, via a maximally-supersymmetric topological quantum field theory with electric-magnetic duality in physics.
[Slides]
Sam Gunningham (Montana State University)
Title: Langlands duality for 3-manifolds
Abstract: I will explain some recent and ongoing work on the state spaces associated to 3-manifolds in the Kapustin-Witten twists of 4d N=4 SYM. This includes joint work with David Ben-Zvi, David Jordan, Pavel Safronov, Monica Vazirani, and Haiping Yang.
[Slides]
Nicolo Piazzalunga (Uppsala University)
Title: The character of M-theory
Abstract: I will present some conjectures for higher-rank K-theoretic Donaldson-Thomas theory on toric three-folds, and some lessons that we learned from working equivariantly on non-compact spaces. Based on 2103.10271, 2111.07663 and upcoming work.
[Slides]
Georgios Linardopoulos (Wigner Research Centre for Physics)
Title: String integrability of defect CFT and dynamical reflection matrices
Abstract: The D3-D5 and D2-D4 probe-brane systems with nonzero worldvolume flux are holographically dual to N=4 super Yang-Mills and ABJM theory in the presence of half-BPS domain walls. The two domain wall systems are thought to be integrable; the evidence comes mainly from the study of correlation functions at weak coupling. In the present talk we show that the string theory duals of these systems are classically integrable. In other words, the string boundary conditions on the probe branes preserve the integrability of the corresponding Green-Schwarz sigma models. This finding suggests that the dual domain wall systems are integrable to all loop orders and for any value of the bond dimension.
Piotr Kucharski (University of Amsterdam)
Title: Quivers for 3-manifolds
Abstract: Since 2017, knots and symmetric quivers are known to be intimately related via BPS spectra. 3 years ago, F_K invariants of knot complements in 3-sphere have been proposed. In this talk I will present how these two threads of research can be combined and what comes as a reward.
[Slides]
Thorsten Schimannek (LPTHE Paris)
Title: Counting BPS states with discrete charges in M-theory
Abstract: In this talk I will introduce a refined notion of Gopakumar-Vafa invariants on singular Calabi-Yau threefolds that generate a discrete gauge symmetry in M-theory. This provides an enumerative interpretation of the A-model topological string partition function on non-commutative resolutions of the singular Calabi-Yau’s. Our starting point will be the observation that a rich source of discrete gauge symmetries in M-theory are Calabi-Yau threefolds with singularities that cannot be crepantly resolved. Just like in the smooth case, one can ask about the multiplicities of BPS states that now carry an additional discrete charge. The corresponding Gopakumar-Vafa invariants provide a discrete refinement of the invariants associated to the smooth deformation. I will argue that they are encoded in the topological string partition functions of the singular Calabi-Yau itself and its various non-commutative resolutions. At the hand of several examples I will illustrate that this phenomenon is generic and that most Calabi-Yau threefolds admit such degenerations and a corresponding refinement of the invariants.
[Slides]
Shi Cheng (University of Warsaw)
Title: Plumbing graphs with matter
Abstract: We discuss abelian 3d N=2 theories T[Ω,U(1)] engineered by plumbing manifolds Ω. The linking numbers of plumbing graphs are interpreted as the effective mixed Chern-Simons levels of 3d N=2 theories with chiral multiplets. There are many equivalent graphs that are related by Kirby moves which are interpreted as integrating out gauge nodes from the perspectives of 3d theories. In the presence of chiral multiplets that are added to plumbing graphs, we show that ST-transformations lead to many equivalent plumbing theories, and hence generalize the scope of Kirby moves. The plumbing graphs with matter can be viewed as certain kinds of quiver diagrams for 3d N=2 theories. One can add superpotentials, which lead to Seiberg-like dualities between plumbing graphs with triangles. One can also Higgs chiral multiplets. Equivalent plumbing graphs suggest dual theories. We show that many 3d theories can be represented as plumbing graphs and hence be able to be constructed by compactifying M5-branes on corresponding plumbing manifolds using the construction of 3d-3d correspondence. This story also relates to the higher-form global symmetry.
[Slides]
Public lecture
Maryna Viazovska (EPFL)
The recording of the lecture can be found here.
Breaking news: on July 5, 2022, Maryna Viazovska was awarded with the Fields medal, the highest recognition in mathematics!
Title: The sphere packing problem and beyond
Abstract: The sphere packing problem is a very natural geometric question and it has a long and exciting history. The original sphere packing problem in dimension 3 is known as Kepler’s conjecture and it was famously solved by Thomas Hales at the very end of the twentieth century. In 2016 the speaker was lucky enough to solve the sphere packing problem in dimension 8 and contribute to its solution in dimension 24. This lecture is aimed for the general public and does not request much prerequisites in mathematics. We will speak about the history of Kepler’s conjecture. Also I explain what is the “dimension” for a mathematician and why it is an extremely useful concept for everyone. Finally, we will talk about the connections between the sphere packing problem and some mysteries of modern physics.
Biogram (in Polish): Maryna Viazovska urodziła się, uczyła i studiowała w Kijowie w Ukrainie. Studiowała na uniwersytecie im. Tarasa Szewczenki oraz w Instytucie Matematyki Ukraińskiej akademii Nauk w Kijowie, a następnie uzyskała stopień magistra na uniwersytecie w Kaiserlautern, oraz stopień doktora w 2013 r. na uniwersytecie w Bonn w Niemczech. Odbyła staże podoktorskie na uniwersytecie Humboldta w Berlinie oraz uniwersytecie w Princeton w USA, a następnie została profesorem w École Polytechnique Fédérale de Lausanne (EPFL) w Szwajcarii, gdzie od 2018 roku kieruje Katedrą Teorii Liczb. Jednym z najważniejszych osiągnięć Maryny Viazovskiej jest rozwiązanie tzw. problemu upakowania sfer w wymiarze 8, a także – we współpracy z innymi matematykami – rozwiązanie tego problemu w wymiarze 24. Za te oraz inne osiągnięcia otrzymała wiele prestiżowych nagród i wyróżnień, m.in. nagrodę Salema, nagrodę Matematycznego Instytutu Clay’a, nagrodę New Horizons in Mathematics. W 2018 została zaproszona jako wykładowczyni podczas Międzynarodowego Kongresu Matematycznego – jest to jedno z najważniejszych wyróżnień dla matematyków. W roku 2019 otrzymała nagrodę Fermata oraz nagrodę Ruth Lyttle Satter przyznawaną przez Amerykańskie Towarzystwo Matematyczne, a w roku 2020 nagrodę Europejskiego Towarzystwa Matematycznego.
Maryna Viazovska at Wikipedia
This public lecture is also a lecture in the “Zapytaj fizyka” series – here is the lecture website.
Information for participants
Recordings and online participation
Plenary lectures during the conference will be recorded and available on our YouTube channel.
It is also possible to listen to the plenary lectures online in real time via Zoom (and ask questions in chat). In order to receive a Zoom link, please submit the following form.
Registration & conference fees
In order to register, you should submit the following form.
Registration deadline: June 1, 2022.
Conference fee:
– standard fee: 1200 PLN
– fee for (PhD and all other) students: 900 PLN
The conference fee covers all coffee breaks, lunches, conference dinner, and conference materials.
In case you would need some financial support, please tick an appropriate box in the registration form and ask a senior scientist (e.g. your supervisor) to send a recommendation letter to stringmath2022@fuw.edu.pl, with “[Your name] – support” in the title of the message.
The registration will be completed after you make a transfer of the conference fee (also taking care of transfer fees, if applicable) to the following bank account:
Account Holder: Uniwersytet Warszawski, ul. Krakowskie Przedmieście 26/28, PL-00-927 Warszawa
Bank Name: Bank Millennium SA, Stanisława Żaryna 2A, PL-02-593 Warszawa
IBAN Code: PL 77 1160 2202 0000 0000 6084 9264
Swift Code: BIGBPLPWXXX
Reference: String Math 2022 [your name]
Location & contact
Faculty of Physics, University of Warsaw
ul. Pasteura 5, 02-093 Warsaw, Poland
https://www.fuw.edu.pl/faculty-of-physics-home.html
Plenary talks will take place in the main lecture hall (lecture hall 0.03) of the Faculty of Physics. Coffee breaks, lunches, and poster presentations will be arranged in the main hall of the Faculty of Physics.
E-mail: stringmath2022@fuw.edu.pl
Travel & transport
Warsaw Chopin Airport – the main airport serving Warsaw. It is located within the city limits, 10 km from the city center, which you can easily reach by a few city buses, a train line, and a taxi.
Warsaw Modlin Airport – another airport, mainly serving budget airlines, located 35 km from the city . It takes around 50 minutes to get to the city center, either by bus and train or a taxi.
Warszawa Centralna Railway Station – the main railway station located in the city center, also serving international trains.
Public transport in Warsaw – the city has a vast transportation network, which includes buses, metro, and trams. You can buy tickets for a single trip (up to either 20 or 75 minutes, with transfers allowed), or multi-day tickets.
Warsaw Public Bike “Veturilo” – one of the largest urban bike systems in Europe. It is a good complement to public transport in Warsaw and allows quick navigation through our city, with over 300 stations and more than 4500 bicycles available. You can register and use at little or (for short enough rides) no cost.
Accommodation
Here are some (relatively) nearby hotels in which participants might choose to stay. For more options you can check Google maps, booking.com, etc.
Hera – guesthouse of the University of Warsaw (budget option)
Ibis budget Warszawa Reduta (*)
Ibis Warszawa Reduta (***)
Campanile Warszawa (***)
MDM Hotel (***)
Radisson Blue Sobieski (****)
Polonia Palace (****)
Visa
Participants requiring a visa to visit Poland are advised to apply for one at Polish consulate well in advance. Information about Polish embassies and consulates can be found here.
Covid regulations and precautions
Official information about covid regulations at the University of Warsaw can be found here. At this moment covid restrictions, concerning visitors and conference organization, have been waived.
Nonetheless, if you have some Covid symptoms, please stay at home or your hotel, and take at least a rapid test (can be bought in a pharmacy). It is also possible to make a PCR test on our campus (it costs 290 PLN, i.e. around 60 EUR), details are explained here:
https://warsawgenomics.pl/en/sars-cov-2/koronawirus-rtpcr
Committees
Organizing Committee
Paweł Caputa
Zygmunt Lalak
Adrian Langer
Miłosz Panfil
Jacek Pawełczyk
Piotr Sułkowski (chair)
Rafał R. Suszek
Scientific Committee
Louis Alvarez-Gaume
Mina Aganagic
David Ben-Zwi
Philip Candelas
Miranda Cheng
Simon Donaldson
Matthias Gaberdiel
Davide Gaiotto
Mark Gross
Albrecht Klemm
Juan Maldacena
Matilde Marcolli
Greg Moore
Hiraku Nakajima
Nikita Nekrasov
Tony Pantev
Leonardo Rastelli
Nicolai Reshetikhin
Sakura Schafer-Nameki
Yuji Tachikawa
Richard Thomas
Katrin Wendland
Steering Committee
Ron Donagi (University of Pennsylvania)
Dan Freed (University of Texas at Austin)
Nigel Hitchin (University of Oxford)
Sheldon Katz (University of Illinois)
Maxim Kontsevich (IHÉS)
David Morrison (University of California)
Hirosi Ooguri (Caltech & IPMU)
Boris Pioline (Université Pierre et Marie Curie)
Joerg Teschner (DESY)
Edward Witten (Institute for Advanced Study)
Shing-Tung Yau (Harvard University)
Gallery
Previous Conferences
String Math 2021 – Instituto de Matemática Pura e Aplicada, Brazil
String Math 2020 – Universities of Stellenbosch and Cape Town, South Africa
String Math 2019 – Uppsala University, Sweden
String Math 2018 – Tohoku University, Japan
String Math 2017 – Universität Hamburg, Germany
String Math 2016 – Collège de France, France
String Math 2015 – Tsinghua University, China
String Math 2014 – University of Alberta, Canada
String Math 2013 – Stony Brook, USA
String Math 2012 – Universität Bonn, Germany
String Math 2011 – University of Pennsylvania, USA
Acknowledgements